El eclipse solar del 21 de agosto y el medio kilo que no fue
Algunos lo han llamado “El eclipse del siglo”; otros, “El gran eclipse estadounidense”. Si bien no será el único de este siglo ni mucho menos el que dure más, parece ser que se le nombra así por razones meramente propagandísticas, sin negar su importancia científica o el hecho inobjetable de la zona que recorrerá la sombra de la Luna sobre la superficie de la Tierra. En cualquier caso, se ha cacareado el huevo.
En varios medios de comunicación se ha hecho énfasis en la supuesta “obscuridad total” que ocurriría en el momento en el cual el disco lunar cubra por completo al solar. Sin embargo, hay que recordar que no se trata de un fenómeno idéntico a la noche pues la corona solar será visible. De hecho, en la mayor parte del planeta, el eclipse será imperceptible o, en el mejor de los casos, parcial. También se habla de que “todos bajaremos de peso medio kilo” [1, 2, 3] y es precisamente esta afirmación la motivación principal de este artículo.
Las personas que vivimos sobre la faz de la Tierra estamos sujetos a la influencia gravitacional tanto de nuestro planeta como de los astros que nos rodean; en especial la de la Luna y la del Sol. Por el simple hecho de tener masa, dos cuerpos experimentan entre sí una acción de atracción mutua, del uno sobre el otro. A esta acción a distancia la llamamos fuerza de gravedad. Nosotros, sólo por poseer cierta cantidad de masa, también generamos una acción de tipo gravitacional, pero es tan pequeña que básicamente no la notamos. Sin embargo, para el caso de los cuerpos celestes, los cuales poseen cantidades de materia enormes, este efecto es muy notorio. Todos los seres que vivimos en la Tierra estamos “siendo atraídos” de forma continua hacia el centro del planeta. De igual forma, la Luna y el Sol generan un efecto de atracción sobre nuestro planeta y sobre todos los seres o cosas que se encuentran en él.
Con el propósito de explicar por qué se dice que “bajaremos de peso”, primero debemos entender dos conceptos físicos: el de “peso” y el de “masa”. El peso es la fuerza con la que la Tierra atrae hacia su centro a los objetos que se encuentran en su superficie. Como sugiere su definición, para especificarlo se debe utilizar una cantidad que indique su magnitud o “tamaño” y en qué dirección actúa. Por otro lado, para especificar la masa, que es la cantidad de materia contenida en un cuerpo, basta con decir su magnitud; no se requiere hacer mención de ninguna dirección. Para expresar cualquier cantidad física, primero ha de definirse un sistema de unidades estándar, como el Sistema Internacional (SI). En él, la unidad de masa es el kilogramo (kg) y la de peso, que es una fuerza, el newton (N). La báscula nos sirve para conocer nuestra masa, pero en realidad mide la fuerza de atracción entre nuestro cuerpo y la Tierra. El resultado que nos muestra es el de la masa expresada en kilogramos o en libras-masa (no se deben confundir con las libras-fuerza) en el sistema inglés de unidades. Digamos que la báscula “hace una operación matemática” para pasar de las unidades de fuerza a las de masa mediante el uso del concepto físico de peso.
Con esta información en mente, revisemos con mayor detenimiento la nota de la NASA en referencia al eclipse total de Sol (traducción al español del texto original)[4]:
“Usando la Ley de la Gravitación Universal de Newton, podemos calcular la fuerza del Sol, la Luna y la Tierra sobre una persona de 80kg. La Tierra aporta 784.1 Newtons de fuerza (176.42 libras), la Luna provee 0.029 Newtons (0.01 onzas) y el Sol provee 0.4633 Newtons (1.6 onzas). Pero, porque la Tierra rota, esto también provee una fuerza centrífuga “anti-gravedad” que también podemos calcular. Así, si añadimos las fuerzas con su dirección correcta, obtenemos una fuerza total gravitacional de 784.1 – 0.0029 – 0.4633 = 783.634 Newtons o 176.317 libras. Entonces, ¡serás aproximadamente 1.7 onzas más ligero!”
La NASA dice en su comunicado que una persona con una masa de 80kg será aproximadamente 1.7 onzas-masa más ligera, lo que equivale a 0.0481942 kg o alrededor de 48.19 g (gramos). Sin embargo, los medios de comunicación entendieron mal las unidades o hicieron las conversiones erróneamente, como sugiere el caso del artículo de la CNN en Español [1]. El problema se agravó probablemente debido a que en el texto de la nota no se distingue explícitamente entre las libras-fuerza (unidad de fuerza en el sistema inglés (lbf)), las libras-masa (unidad de masa en el sistema inglés (lbm)), ni tampoco entre sus submúltiplos (onzas-fuerza y onzas-masa). Todas las cantidades que siguen a las magnitudes de las fuerzas expresadas en newtons tienen unidades de fuerza, ya sea libras-fuerza u onzas-fuerza. Únicamente cuando se dice “1.7 onzas más ligero” se hace referencia a unidades de masa; en este caso, onzas-masa. Por consecuencia, muchos medios comunicaron equivocadamente que “perderemos alrededor de medio kilo”. Además, el cálculo que se divulgó a través de la página de la NASA es aplicable única y exclusivamente para una persona de 80kg. Personas con otra masa experimentarían cambios distintos al mencionado.
Antes de comprobar las cantidades proporcionadas en el comunicado de la NASA, démonos a la tarea de hacer algunas precisiones adicionales.
La Tierra gira en torno al Sol en una órbita elíptica, lo cual quiere decir que la separación que existe entre ambos cuerpos celestes es variable. Sin embargo, por simplicidad, suele tomarse un valor promedio de esta distancia conocido como Unidad Astronómica o UA. Lo mismo pasa con la Luna. Nuestro satélite natural no gira alrededor de la Tierra en una órbita circular, ni tampoco se mantiene en un mismo plano al trasladarse alrededor de nuestro planeta; es decir, se acerca y se aleja, además de que “sube y baja”. Su comportamiento se asemejaría al que se podría observar al seguir la trayectoria que describiría un punto pintado sobre el aro que utiliza una persona cuando juega el “hula hula”. Es por ello que también puede recurrirse al uso de un valor promedio para describir la distancia que existe entre los centros de la Tierra y de la Luna. Y por último, nuestro planeta no es perfectamente esférico; de hecho, es achatado en los polos, haciendo que se vea más gordito en el ecuador. Por consecuencia, el radio de la Tierra tampoco es el mismo cuando cambiamos de latitud. Recordemos que la latitud es la coordenada terrestre que nos indica si estamos cerca o lejos del ecuador (la latitud 0º corresponde al ecuador y la 90º a los polos).
A continuación, tratemos de entender cómo se suman las fuerzas que actúan sobre una persona que observa el eclipse total de Sol.
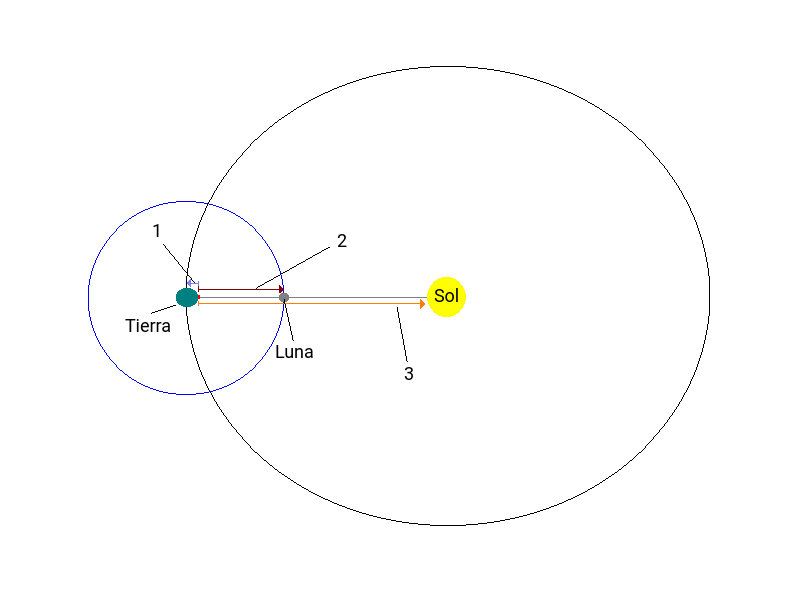
La figura 1 presenta una vista “desde arriba” de las posiciones del Sol, la Tierra y la Luna en un momento en el cual se encuentran perfectamente alineados, como cuando ocurre un eclipse total de Sol. También muestra tres flechitas con sus respectivos números. La 1 representa la dirección en la que actúa la fuerza que la Tierra ejerce sobre una persona parada en su superficie; la 2, la dirección de la fuerza que ejerce la Luna sobre la misma persona y la 3, la dirección de la fuerza que ejerce el Sol sobre, de nuevo, la misma persona. Las tres fuerzas actúan sobre una misma línea, razón por la cual les llamamos fuerzas “colineales” y pueden ser sumadas tomando en cuenta el sentido en el cual actúan. Así, la fuerza 1, que equivale al peso de la persona, actúa hacia la izquierda y las fuerzas 2 y 3 en la dirección opuesta. Las fuerzas que operan en una misma dirección se suman; por un lado, todas las que apuntan a la izquierda y por el otro, todas las que van hacia la derecha. Finalmente, la fuerza neta que experimenta la persona se obtiene de restar el resultado de sumar las fuerzas producidas por la Luna y el Sol (F2 + F3), de la fuerza que ejerce la Tierra sobre la persona (F1). Matemáticamente, se expresa de la siguiente manera:
(F1) – (F2 + F3) = FResultante
La fuerza resultante equivaldría al “nuevo peso” que tendría la persona cuando está sujeta a las acciones gravitacionales de la Tierra, la Luna y el Sol al mismo tiempo.
Ahora, partamos de la Ley de la Gravitación Universal de Newton, que dice que la fuerza con la que dos cuerpos se atraen es directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que las separa. En términos matemáticos, la magnitud de esta fuerza está dada por la ecuación:
donde G es la constante de gravitación universal, Ma y Mb son las masas de los cuerpos y r es la distancia entre sus centros.
La tabla 1 presenta las cantidades físicas y los valores promedio de las distancias entre la Tierra, la Luna y el Sol, datos que deben sustituirse en la ecuación de la Ley de la Gravitación Universal para hallar las distintas fuerzas que actúan sobre la persona que presencia el eclipse. La tabla 2, por su parte, muestra los resultados obtenidos tras efectuar la sustitución. Las fuerzas encontradas difieren de las que muestra la NASA, excepto por la que corresponde al peso de la persona, que es de 784.08N (ojo: la NASA redondeó la cifra decimal, quedando en 784.1N). La razón de la diferencia estriba en que en la nota de la agencia espacial, las magnitudes de las fuerzas entre la persona y el Sol y la persona y la Luna se obtuvieron a partir de los valores reales, no promedio, de las distancias entre dichos cuerpos en el momento del eclipse y, además, porque supusieron que la persona no se encontraba en el ecuador. No obstante, al calcular su peso, sí la situaron en esta posición geográfica (ecuador), lo cual constituye una inconsistencia en su procedimiento. Como puede observarse en la tabla 1, se incorpora la famosa “fuerza centrífuga”, la cual se menciona en el comunicado. Con estos valores, se encuentra que, para una persona de 80kg, la masa que aparentará perder será de aproximadamente 48.87g. Tenga presente que en realidad, la persona no pierde masa sino que disminuye su peso por la acción de las fuerzas combinadas de la Luna, el Sol y la fuerza centrífuga. No obstante, puesto que la báscula mide la fuerza entre la Tierra y la persona sin conocer los efectos gravitaciones producidos por el eclipse, ésta detectará un peso menor, el cual asociará a una masa menor.


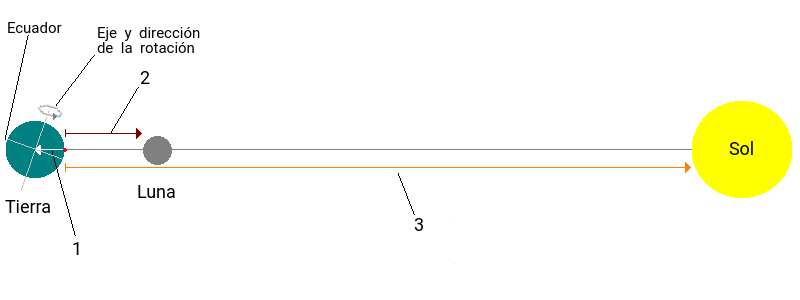
La tabla 3 muestra las cantidades físicas y los valores reales de las distancias entre los astros involucrados durante el eclipse total de Sol; datos que deberán usarse en la ecuación de la Ley de la Gravitación Universal de Newton con el fin de encontrar los valores de las fuerzas implicadas (ver fig. 2). Las distancias fueron obtenidas mediante el programa computacional KStars [5]. La tabla 4 muestra las magnitudes calculadas para cada una de las fuerzas consideradas. Como se puede ver, además de ser distintos a los encontrados en el caso previo, las correspondientes a las fuerzas debidas a la Luna y al Sol concuerdan con los que la NASA publicó en su comunicado. No así el peso, ya que este último se calculó considerando que la persona se encuentra en la latitud en la que la duración del eclipse total de Sol es máxima y no en el ecuador. De nuevo, se toma en cuenta la fuerza centrífuga para el cálculo. Así, la masa que aparenta perder una persona de 80kg debido al fenómeno es de aproximadamente 47.56g. La diferencia entre el dato que proporciona la NASA (48.19g) y el que aquí se presenta (47.56g) se debe a que el cálculo presentado en la página de la agencia espacial no toma en cuenta la latitud en el procedimiento de obtención del peso de la persona y al parecer, tampoco la fuerza centrífuga.


Por último, variemos un poco la masa de la persona que estará sujeta a la influencia gravitacional de la Luna y el Sol en la latitud y momento adecuados para ver el eclipse total de Sol. Un individuo de 50kg aparentará perder una masa de 29.72g; alguien de 60kg, 35.67g; de 70kg, 41.62g; de 90kg, 53.51g; de 100kg, 59.45g y de 110kg, 65.40g. Lo que podemos ver es que cuanto más masiva sea una persona, mayor peso perderá. Enfaticemos que no se pierde masa, se trata sólo de un efecto aparente; lo que sí se reduce, al menos momentáneamente (mientras dura la fase total del eclipse solar), es el peso. Así pues, pareciera un acto de “justicia cósmica” el que los más gorditos serán los que más bajarán de peso.
Tras todo lo expuesto, debe ser claro que el decir que “todos bajaremos medio kilo” constituye un error desde el punto de vista físico. Lo que se intenta decir es que, durante el eclipse, el efecto gravitacional combinado del Sol y la Luna hará que nuestra báscula mida un peso menor que el habitual, la cual nos dará una medición alterada de nuestra masa, aparentando ser menor que la real. Además, podemos concluir que no es cierto que todos perderemos la misma cantidad de peso el día del eclipse. De hecho, sólo las personas que se encuentren en la latitud adecuada [6], en el momento adecuado (durante el eclipse total de Sol) y que tengan 80kg aparentarán perder 47.54g (de ninguna manera medio kilogramo). Si nos encontráramos fuera de ese punto o si no tuviéramos los 80kg, como ya hemos visto, experimentaremos una disminución diferente de nuestro peso.
Algunas consideraciones finales
Tome en cuenta que la explicación precedente tiene el propósito de arrojar luz sobre el comunicado aparecido en la página de la NASA dedicada al eclipse solar del 21 de agosto de 2017. En este sentido, se ha buscado exponer el razonamiento implicado en las declaraciones plasmadas en él y no resolver el problema físico en un sentido estricto. Asimismo, se intenta desmentir la información que los medios de comunicación divulgaron erróneamente.
Probablemente por razones didácticas, el comunicado parte de una serie de suposiciones que buscan simplificar el análisis de las fuerzas que actúan durante el eclipse, a fin de facilitar su comprensión por parte del público en general. No obstante, tenga presente que el fenómeno es mucho más complejo en la realidad.
¿Significa esto que todo lo dicho es erróneo? No exactamente. En su lugar sería preferible decir que los resultados son válidos únicamente dentro del marco de las aproximaciones que se realizaron para obtenerlos. Por ejemplo, el autor del comunicado asumió tácitamente que tanto el Sol, la Luna y la Tierra se encuentran en posiciones estáticas; es decir, que no cambian su ubicación con el transcurrir del tiempo. Como consecuencia, la Tierra no gira en torno al Sol ni la Luna en torno a la Tierra, permitiendo así omitir los efectos dinámicos producidos por el movimiento de dichos astros. Evidentemente, en el escenario real es imposible ignorarlos. Por otro lado, también supuso que en un momento diferente al del eclipse, la Luna y el Sol no influían de ninguna manera sobre el peso de la persona, lo cual, por supuesto, no puede ocurrir de esta manera. Ambos astros ejercen su influencia permanentemente. La consecuencia inmediata de ambas suposiciones se manifiesta como una sobrestimación del efecto de reducción del peso de la persona, pero conllevan la ventaja de permitir la explicación de la fuerza de gravedad que ejercen los cuerpos cósmicos en un nivel básico, aunque no entraremos aquí en detalles sobre su pertinencia.
Para concluir, quizá quede pendiente el responder una pregunta. Si durante el eclipse solar una persona de 80 kg decidiera utilizar una báscula, ¿realmente mediría una reducción de 47.54g?
Lamentablemente, la respuesta es no. Sin alejarse demasiado del contexto de las aproximaciones asumidas en el comunicado, puede realizarse una mejora significativa; al determinar el peso de la persona en un momento diferente al del eclipse (antes de él, por ejemplo), considerar que tanto el Sol como la Luna ejercen sobre ella una atracción gravitacional que es parecida en magnitud a la que se obtiene en el momento en el que el eclipse alcanza su fase total. De este modo, se minimiza la diferencia entre la magnitud del efecto gravitacional producido en la fase total del eclipse y la que corresponde a ese otro momento. De hecho, en el contexto de tal aproximación, disminuye a unas centésimas de gramo; una cantidad imperceptible para todo fin práctico. Conviene mencionar también que cada vez que hay una luna nueva, la posición de la Luna y del Sol respecto a la Tierra es similar a la que ocurre durante el eclipse solar, produciendo cada 28 días un fenómeno gravitacional muy parecido.
Finalmente, los entusiastas que deseen saber cómo se obtuvieron los valores que presentó la NASA, pueden remitirse al documento en formato PDF que se incorpora más abajo.
Como siempre, invito a mis compatriotas a estudiar, a informarse y sobre todo, a no dejarse llevar por las noticias, que, por más seductoras que parezcan, podrían estar completamente erradas.
Síganme en Mastodon:
https://social.politicaconciencia.org/@Maya
Bibliografía
[1] http://cnnespanol.cnn.com/2017/08/10/todos-pesaremos-medio-kilo-menos-este-21-de-agosto/
[2] http://www.vanguardia.com.mx/articulo/el-eclipse-del-21-de-agosto-nos-hara-bajar-de-peso
[4] https://eclipse2017.nasa.gov/what-gravitational-effects-happen-during-total-solar-eclipse
[5] https://edu.kde.org/kstars/
[6] https://eclipse2017.nasa.gov/sites/default/files/interactive_map/index.html

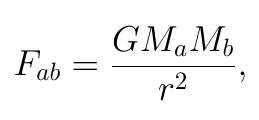




Me ha encantado esta cátedra que demuestra cómo compartir el conocimiento de una manera tan natural y didáctica. La autora de este artículo nos proporciona todo lo necesario para entender y comprender mejor lo que sucederá durante este cacareado Eclipse.Su compromiso de transmitir objetiva y verazmente los acontecimientos en torno al evento que nos ocupa me deja un grato sabor de boca, pues aún siendo un neófito en la materia, he podido comprender su maravillosa explicación. Siempre me ha gustado leer artículos que me enseñen e informen a la vez. Felicito a la autora Maya por su excelente artículo. Tanto me gustó que quiero compartirlo con niños y jóvenes que no saben exactamente que es lo que va a pasar. Oír las explicaciones que nos dan en la radio o en algunos medios escritos, realmente dan pena, pues sólo se deforma la verdad y la realidad del evento. Se dicen tantas cosas absurdas en torno a este Eclipse que francamente no se entiende por qué lo están manejando de esa manera. Bueno, Maya lo dice; en E.U. todo se mercantiliza. Me felicito por haber leído tu excelente clase artículo.
Muchas gracias por tan sentido comentario 😀
Agradezco a mi maestra la ensenanza tan clara del eclipse total de sol y sus aparentes consecuencias en el peso de una persona. Reyna
Me da mucho gusto que te haya parecido útil e interesante. Un abrazo fuerte.
No me había encontrado con un artículo así que explicara lo que realmente “nos” pasará durante el eclipse; pero ahora me queda claro que ni serán dos kilos, ni medio, ni será a todos ni en todas partes. Más curioso me resulta la forma en la que los medios de comunicación manejan o tergiversan incluso la información científica y académica. Quizá por eso tendemos aún más a la ignorancia. ¡Qué horror! Eso sí, me quedó una duda de tu artículo: habla de masas humanas, en particular de uno de 80 kg, pero, sobre entiendo que, ¿todos los cuerpos masivos (o solo aquellos según el lugar y altura en donde se encuentren al momento del eclipse) experimentarán un cambio en su peso o sólo los seres vivos o humanos con determinadas características? Es decir, ¿también una piedra en las circunstancias adecuadas va a experimentar ese cambio? ¿Un venado? ¿Un coche? Es decir, ¿esa parte misma de la tierra y ciertos objetos masivos en ella? ¿O es cosa sólo de humanos? Seguro que es una pregunta muy tonta, pero me dio curiosidad. Gracias ?
Si Tocino, los efectos gravitacionales se dan sobre todas las cosas, animadas o inanimadas, que estén sobre la Tierra. Eso sí, en cada caso tienen una magnitud distinta. Es interesante notar que, en este caso, la fuerza de gravedad actúa exactamente igual sobre una piedra de 80kg que sobre un humano con la misma masa.
Muchas gracias por la aclaración y por responder. No pensé que lo harías. Gracias por tomarnos en serio. Atte, Tocino.
Realmente importante y bien fundamentado el artículo de Maya. Me era incomprensible la causa de porqué podríamos pesar menos durante el eclipse, Ahora me parece entendible la influencia de los astros sobre nosotros durante su conjunción. Además veo el gran interés despertado por el tema con el número de entradas registrado en este artículo.
Muchas gracias por el comentario Gladys. Me complace saber que te pudo ser de ayuda para comprender un poquito mejor esta parte de la física newtoniana. Sin duda el artículo ha sido llamativo para la gente y es bueno saber que es un tema de interés.